かれこれ一年近く前になりますが、下記で 2-3 木を実装した話を書きました。
この記事の冒頭でも書いたのですが、もともとは平面走査法を試したくて、そのためのデータ構造として 2-3 木を実装したという流れでした。ずいぶんと時間がたってしまいましたが、やっと平面走査法の実装にめどが立ったので、実装の経緯などについてメモっておきます。
なお、実装時の環境は以下の通りでした。
- WIndows 11 22H2 上の WSL2, Ubuntu 22.04.2
- Python 3.11.4
前回と同様に、 Windows 上の VSCode から WSL にリモート接続して開発してます。
平面走査法について
平面走査法そのものは、ネットを調べればいくらでもいい記事が見つかるので、ここでは詳しく説明しませんが、この記事を書くにあたり、簡単に説明しておきます。
- 平面上に複数の線分(直線や半直線ではなく、限られた長さを持つ線分)があるときに、全部の線分同士の交点を求めたい場合に使います
- 線分を2つ選んで、交点を求める、という処理を、すべての組み合わせについて行えばもれなく見つけることができます
- でも、これだと効率が悪いということで考えられたのが、平面走査法、ということだそうです
で、平面走査法というのは大雑把にいうと
- 例えば、 X 軸に垂直な線分(走査線)を用意します
- 走査線を X 軸に沿って、動かします
- 走査線と交差する線分を求めます
- 走査線と線分の交点の y 座標が小さい方から並べます
- このとき、走査線上で隣り合う線分同士の組み合わせに対してのみ、交点があるか求めます
- これを繰り返すことで、もれなく交点を求めます
という方法になります(詳しくは後述の参考書籍やググってもらえればと思います)。
走査線を動かすのは、連続的に動かす必要はなく、走査線上の線分の並びに変化が生じる特定の位置のみを考えればよいとのことです。 具体的に走査線を設定する位置としては
- 線分の端点
- 交点
に限定できます。線分の端点では、走査線上の線分として、追加(または削除)が起き、交点では、交点通過前後で線分の並びに入れ替わりが生じるためです。
で、どこでデータ構造を使うかというと
- 走査線を移動させる位置(線分の端点および交点)を管理する
- 走査線上にある線分の並びを管理する
ために必要になります。このデータ構造として、 2-3 木を使ってみたということになります。
詳しくは、参考にしている『データ構造とアルゴリズム』などをご覧ください。
実装
平面走査法の実装の前に、点および線分を管理するためのクラスを作成しておきます。このあたりのクラス構成は、
Blogopolisから学ぶ計算幾何 記事一覧 | gihyo.jp
などを参考にさせていただきました。
点および線分クラスが定義できれば、平面走査法の実装はこれらのクラスを利用して、上記の処理をそのままコードにすればOKです。今回は、走査線を X 軸に垂直な線とし、X軸の負の方向から正の方向に向かって、走査線を移動させていく、という前提とします。
ただ、2-3 木を利用するために、点および線分クラスを利用したデータ構造(2-3 木のノードが保持するデータ構造)を定義してやる必要があります。それについてだけ、触れておきます。
『走査線を移動させる位置(線分の端点および交点)を管理する』ためのデータ構造
上記の『走査線を移動させる位置(線分の端点および交点)を管理する』ための 2-3 木としては、
- x 座標をキーとする
というデータを管理すればよいはずです。この形としておけば、走査線が X 軸の負の方向から正の方向に移動する際に、各線分の端点および交点位置を順番に選び出すことができます。
とはいうものの、走査線を移動させる際にその位置が、左の端点か右の端点か、交点かを区別する必要があるので、そのための情報を持たせます。
- 左の端点では、走査線上に線分が追加される
- 右の端点では、走査線上から線分が除外される
- 走査線上の線分の並びが、交点前後で入れ替わる
ということが起きるからです。また、交点の場合は、どの2線分に対する交点であるのかという情報も必要になります。
これらを踏まえて、 2-3 木で管理するためのデータ構造として
@unique class EventType(Enum): """イベント種類の enum 平面走査法のイベント種類を表す """ LEFT = auto() # 左端点 CROSS = auto() # 交点 RIGHT = auto() # 右端点 @dataclass class BNode: """平面走査法で用いるイベント管理するための Node 要素 """ eventType: EventType # イベント種類 pt: Point # イベントに対する Point, この X 座標がメインのキー ls: LineSegment # Point が存在する線分 ls2: LineSegment | None # イベントが交点の場合の2つ目の線分 lnId: int | None # 線分 ID, 端点追加時のみ割り当てる
というものを定義しました。
そのうえで、このデータ構造体を内部に持って、 2-3 木の Leaf クラスを継承した葉クラスを作成します。
class LeafB(Leaf[BNode]): def __init__(self, val: BNode, parent: Node[BNode] | None): super().__init__(val, parent, self._get_leafb_key, self._comp_leafb_key)
2-3 木の大小関係を決定するのは、実際には、 self._comp_leafb_key で定義された関数になります。
『走査線上にある線分の並びを管理する』ためのデータ構造
同様に、『走査線上にある線分の並びを管理する』ための 2-3 木としては、
- y 座標をキーとする
というデータを管理すればよいはずです。ですが、y 座標は走査線の位置に応じて変化していくので、直接 y 座標を持ったデータ構造では不十分です。このため、『走査線上にある線分』を管理するということから、線分そのものを持ったデータ構造としておき、走査線の位置に応じて、 y 座標を計算することを考えます。
これらを踏まえて、 2-3 木で管理するためのデータ構造として
@dataclass class ANode: """平面走査法で用いる走査線上の線分を管理するための Node 要素 """ ls: LineSegment # Point が存在する線分, 走査線上における線分の y 座標をキーとする
を定義します。
この2-3木は、走査線の位置に応じて、各線分の y 座標値を計算する必要があるので、葉クラスとしては、
@dataclass class Sweepline: x: float # 走査線の x 座標 class LeafA(Leaf[ANode]): _delta_x : float = -1 * _DELTA def __init__(self, val: ANode, parent: Node[ANode] | None, sweepline: Sweepline): super().__init__(val, parent, lambda v: str(v.ls.calcYIfExist(sweepline.x)), self._comp)
のような形で、走査線クラス(Sweepline)を引数にとるようにしておきます。
気になる点
さて、アルゴリズム自体は、上記の参考図書などを読めばいいのですが、実際に実装してみると、いくつか気になることがでてきました。
ここでは、それらについて挙げておきます。ベースにしている参考書籍で紹介されている方法を元にした場合、
- 同じ走査線上に複数の線分の端点や交点が存在している場合に、どうすれよいのか?
- 線分上に別の線分の端点が存在している場合、どう処理すればよいのか?
- 走査線と平行な線分がある場合、どう処理すればよいのか?
といった問題については、触れられていません。が、実際にこれを利用しようとすると対応しておく必要があると思われます。
また、走査線上に存在する線分を管理するにも 2-3 木を使っているため、
- イベントにより走査線を動かした場合の交点の入れ替え処理をどうするのか?
という点も気になります。
以下で、これらの問題にどう対応したかを書いておきます。ちなみに、実際には最初にこれらの問題を無視して実装を書いて、その後テストケースを追加しながら、アルゴリズムを検討していきました。最初から完璧なものを作ろうとすると嫌になってきますからね。
交点の入れ替え処理
交点の入れ替え処理ですが、当初は、走査線上の線分を管理する 2-3 木における、葉(キー)の大小判定処理でなんとかなるかな?と考えていました。ですが、いろいろなテストケースを考えて試してみると、どうもうまくいきません。
ということで、最終的には、2-3 木に、2つの葉を入れ替えるためのメソッドを追加してそちらで対応するようにしました。
ただし、葉の入れ替えを行っても、木の再構築は行わずに、それぞれの葉の親に当たる中間ノードの left_max や mid_max の更新のみを再帰的に行うようにだけしました。
走査線上の複数の端点や交点の扱い
走査線上に端点と交点が存在しているような場合があります。

左図の x = 0.5 のところや、右図の x = 1.25 のところなどです。
走査線上に複数の端点がある場合や、

走査線上に複数の交点がある場合もあります。

今回の実装では、走査線を進めていく方向(今回の実装だと、 X 軸の負から正の向き)に従って、線分の端点をイベントとして管理します。その管理にも 2-3 木を使うため、単純に端点の x 座標値をキーにするだけだと、キーの重複が起きてしまい、2-3 木で扱えなくなってしまいます。
そこで、今回は x 座標値に加えて、 y 座標値でもキーの判定を行うようにして、同じ走査線上にある場合は、 y 座標が負から正の向きにイベントを処理するようにしました。
また、同様に、ある x 座標値の走査線上に交点が存在する場合、先に交点のイベントを処理して、線分を入れ替えておかないと、線分の組み合わせにより交点を求める処理の際に正しい組み合わせにならないため、イベント種類によっても、異なるキーとして扱うようにしました。
線分上に別の線分の端点が存在している場合の扱い
線分が交差しているのではなく、一方の線分の途中に別の線分の端点があるような場合です。

これらについては、交点を求めた際に、既に端点として存在しているか否かをチェックして、存在している場合は交点イベントとして追加しないようにすることで対応します。
また、異なる線分の端点同士が重なっているというケースも存在します。

これについては、端点の座標だけでなく、線分にIDを割り振っておき、IDが異なれば、別の線分の端点であるからイベントとして取り扱うようにします。
最終的な比較関数
上記で検討したことの多くは、2-3 木の葉の比較関数で対応しています。この記事で実装した 2-3 木の場合は、同じキーがあると既に葉が存在していると判定して追加を行いません。
このため、比較関数で正しく区別ができないと、端点および交点をイベントとして追加できず、ひいてはその端点に関する線分が扱われないので、交点算出から抜け落ちることになるためです。
最終的な比較関数がどのようになったかは、 Github のコードをご確認ください。
走査線に平行な線分の扱い
これは、最初は、対象の線分全体(とうか座標系)を回転させれば、考慮しなくてもいいんじゃないかな?と思ってました。
ですが、こちらのPDFの最初の事例を見てみて、走査線に平行な線分を検出したら、その線分の端点(上下の点)を通る水平な線分を作って、走査線上の線分リストからその2つの水平な線分の間にあるものを抽出すれば、それが交点になる、ということに気が付きました。
ということで、走査線に平行な線分については、これで特別に対応することにします。
実装結果
上記を含めた実装結果は、2-3 木とともに、こちらのリポジトリに上げておきますので、ご興味のある方はご参考にしてください。
あと、テストケースが実際にどういう線分になっているかは、下記の gist などを参照してください
試し
一応、上記を考慮しながら頑張って実装してみました。こんな感じのデータを与えて計算してみると、
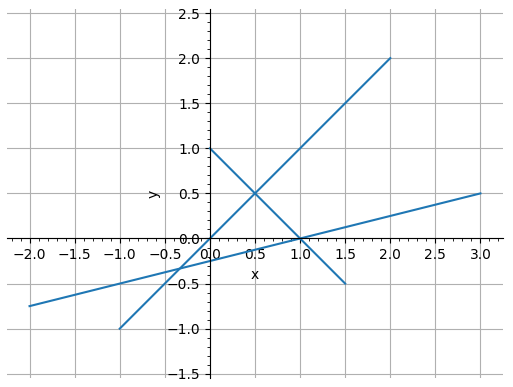
(-1/3, -1/3)
(0.5, 0.5)
(1, 0)
のように、正しく線分の交点を求めることができました。
その他にも、こんな感じで与えても

こんな感じに、座標軸に平行な線分でも

交点を正しく求めました。
まとめ
とりあえず試した範囲で、正しく動作していそうなので、一応実装できたことにしたいと思います。
ただ、このアルゴリズムの場合、3線分以上が 1 点で交差する場合に対応できません。元の参考書籍に記載しているアルゴリズムの時点でその制約はあるのですが、求めることができないにしても検出する方法があるといいなと思ったのですが、ちょっとそこまでできませんでした。
にしても、書籍にさっと書いてあっても、いざ、実際に自分で実装してみると、なかなか手ごわいですね。でも、自分で組むのはやっぱり楽しいもんです。次は何しようかな。
2024/9/17 追記
上記のテストデータをグラフとして描画するのに、 Google Colaboratory を利用しました。下記にもまとめたので、ご興味のある方はみてもらえればと思います。
